Confident Declaration: One-Step Polygon Area Solution Revealed
I recall a moment when I argued with my son about my capability to determine the area of a polygon in a single operation within half a minute, whereas he would solve it through multiple steps, as they instructed him at school.
I won!
And since I brought it up, I’d like to share with you how, by just employing a singular equation, you can precisely compute the area of a polygon, eliminating the need to dissect the shape into multiple, simpler figures.
Nevertheless, there’s a vital requirement for these kinds of polygons: each point must possess whole number coordinates, meaning it must be precisely positioned at a grid intersection.
A grid is a plane with cells on which a shape is drawn. An intersection represents where the gridlines meet.
The grid can have any measuring unit, because the area is quantified in square units of the measurement chosen. If the cell is 1×1 cm, then that’s 1 sq. cm, 1×1 m is 1 sq. m, and so on.
Thus, there’s a truly straightforward equation that connects the area of any polygon to the count of grid intersections situated along the shape’s lines and within the figure itself. The equation was discovered by the Austrian mathematician Georg Alexander Pick in 1899; therefore, it bears the name Pick’s equation (theorem):
S = G/2 + B – 1
where:
- S is the polygon’s area;
- B — number of points inside the shape (units);
- G is the number of points situated at the shape’s corners and along its lines (units).
To illustrate, let’s consider a sophisticated polygon. We need to compute the area of the shape below:
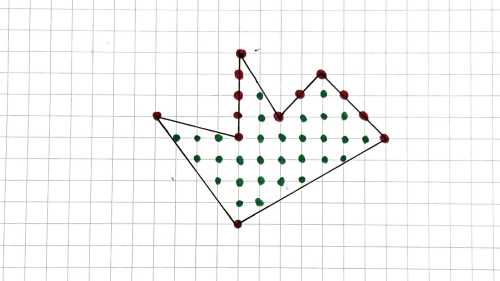
We tally the points located inside, at the corners, and on the shape’s lines.
There is a firm condition in Pick’s equation: it considers only points with integer coordinates—that is, those positioned precisely at the grid lines’ crossings.
We have: G=13, B=30. Now it is sufficient to substitute the values into the equation and we get: S=G/2 + B — 1 = 13/2 + 30 -1 = 35.5 sq. units.
Success! The area equals 35.5 squares. You can verify everything and you will be pleasantly surprised!
The benefits are that such an equation is easy to remember and straightforward to implement! There is, certainly, a drawback, as I previously stated – the equation does not yield a correct answer if even one of the polygon’s corners is located outside the grid intersection (lacks integer coordinates).
My son is already successfully utilizing this equation in school lessons and rapidly obtaining answers, although some educators do not endorse this strategy and still favor adhering to the established method: break the polygon into basic forms, calculate their areas using standard equations, and sum them to arrive at the result.
Nevertheless, I still believe the equation is valuable for swift calculations. Be sure to inform your kids about it!
I sincerely trust you appreciated the article!
